Linearne odvisne in neodvisne vrstice: definicija, primeri

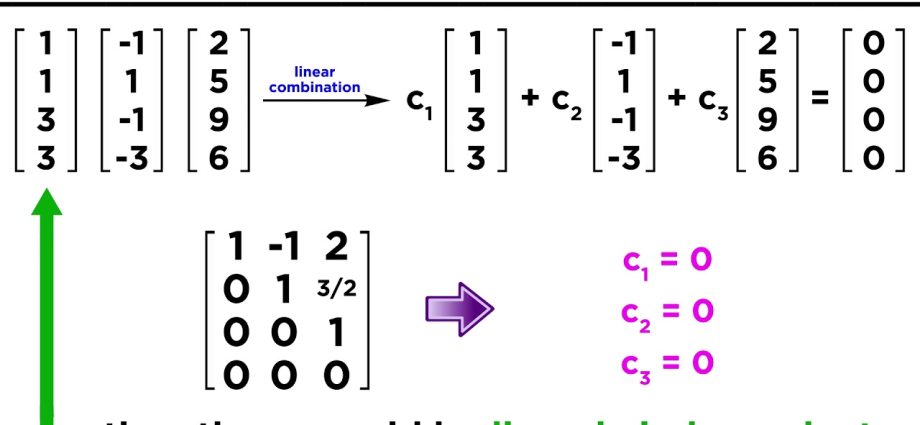
V tej publikaciji bomo obravnavali, kaj je linearna kombinacija nizov, linearno odvisnih in neodvisnih nizov. Navedli bomo tudi primere za boljše razumevanje teoretične snovi.

Definiranje linearne kombinacije nizov

Linearna kombinacija (LK) izraz s₁z₂, …, s_n matrica A imenovan izraz naslednje oblike:

αs₁ + αs₂ + … + αs_n

Če vsi koeficienti α_i so enake nič, torej je LC nepomembno. Z drugimi besedami, trivialna linearna kombinacija je enaka ničelni vrstici.

Na primer: 0 · s₁ + 0 · s₂ + 0 · s₃

V skladu s tem, če je vsaj eden od koeficientov α_i ni enako nič, potem je LC netrivialno.

Na primer: 0 · s₁ + 2 · s₂ + 0 · s₃

Linearno odvisne in neodvisne vrstice

Sistem strun je linearno odvisen (LZ), če obstaja njihova netrivialna linearna kombinacija, ki je enaka ničelni črti.

Iz tega sledi, da je lahko netrivialni LC v nekaterih primerih enak ničelnemu nizu.

Sistem strun je linearno neodvisen (LNZ), če je samo trivialni LC enak ničelnemu nizu.

Opombe:

• V kvadratni matriki je sistem vrstic LZ le, če je determinanta te matrike enaka nič (o =
• V kvadratni matriki je sistem vrstic LIS le, če determinanta te matrike ni enaka nič (o ≠ 0).

Primer problema

Ugotovimo, ali je sistem nizov {s₁ = {3 4};s₂ = {9 12}} linearno odvisen.

Sklep:

1. Najprej izdelajmo LC.

α₁{3 4} + a₂{9 12}.

2. Zdaj pa ugotovimo, katere vrednosti naj sprejmejo α₁ и α₂tako da je linearna kombinacija enaka ničelnemu nizu.

α₁{3 4} + a₂{9 12} = {0 0}.

3. Sestavimo sistem enačb:

4. Prvo enačbo delite s tri, drugo s štiri:

5. Rešitev tega sistema je katera koli α₁ и α₂, S α₁ = -3a₂.

Na primer, če α₂ = 2POTEM α₁ = -6. Te vrednosti zamenjamo v zgornji sistem enačb in dobimo:

Odgovor: torej črte s₁ и s₂ linearno odvisen.